top of page

Introduction to Quadratics
Quadratic equations in Factored Form
y= a(x-r) (x-s)
How to find zeros from Factored Form
When you are trying to find the zeros or the x-intercept for your parabola, just sub 'y' as a zero. Therefore (x-r) is equal to 0, and (x-s) is equal to zero.
Now that you've substituted 'y' as zero, you can see that 'r' is qual to 'x'
y=(x-r)
0=(x-r)
0+r=x-r+r
r=x
You can do the same for
y=(x-s), so you can figure out both the zeros/x-intercepts.

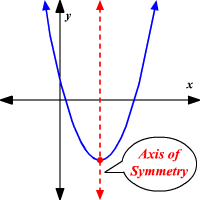
How to find the axis of symmetry ("x") from factored form
Now that you know how to solve for the two x-intercepts, you are going to use those two values to find out the axis of symmetry using this easy equation.
y=(s+r)/2
This equation will give you the x value of your vertex, and that will leave you with the y value to find out, meaning the Optimal Value.
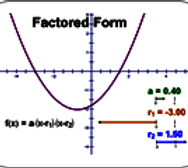
How to find the Optimal Value from Factored Form
Now that we know our x value, we're going to substitute it into the original equation [y=(x-r) (x-s)] and solve until we find our y-intercept.
Consider This...
Label the x-intercepts and the vertex of the equation y= (x-r) (x-s)
y= (x+2) (x-6)
1. First lets figure out the zeros or also known as the x-intercepts
y=(x+2)
0=(x+2)
0-2=(x+2-2)
-2=x
y=(x-6)
0=x-6
0+6=x-6+6
6=x
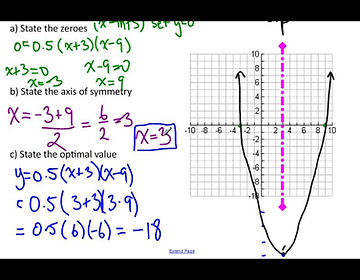
2. Secondly, you need to figure out the axis of symmetry which is the x value for the vertex, so that we can eventually find out the Optimal Value.
x=s+r/2
x=6-2/2
x=4/2
x=2
3. Now that we've found the x value of the vertex, you can easily figure out the y value by subbing the x value into the original equation.
y=2(2+2) (2-6)
y=2(4) (-4)
y=2(-16)
y=-32

Graph and label the Zeros, Axis of Symmetry, and the Vertex
bottom of page