top of page
Introduction to Quadratics
Vertex Form
Y=a(X-H)2+K
y=a(x-h)2+k
This is the Vertex Form of the quadratic equation.
(h,k) is the vertex of the parabola
-
'h' repersents a horizontal translation (how far left, or right the graph has shifted from x=0)
-
'k' repersents a vertical translation (how far up, or down the graph has shifted from x=0)
-
'a' represents the direction of opening and the shape of the parabola

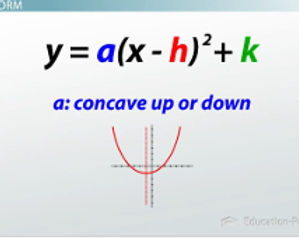
$95
per hour
What is a Step Pattern & how does it effect my Parabola
With a Parabola that has no stretch or where there is no 'a' value, then you follow a regular Step Pattern
This is the regular Step Pattern. It determines the stretch of your parabola, but always remember 1 up and 1 over, 2 up and 4 over, etc.
If your parabola does have a stretch for example, y=2(x+2)2-4, you would
multiply your x squared value by the value of the stretch. In this case the stretch is 2, so it would be 1 over and 2 up, 2 over and 8 up, 3 over and 18 up.
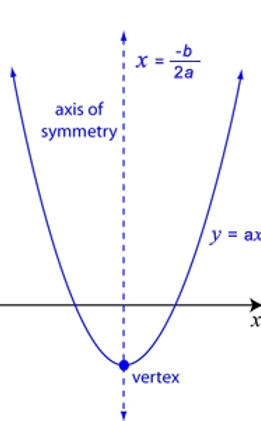
Lets find our Vertex and Axis of Symmetry
Finding the vertex is really easy, it is represented like this (x,y). The x-coordinate is equal to the h value within the equation and the y-coordinate is equal to the k value within the equation. Always remember that a negative h value in the equation means the x value is positive, and a positive h value in the equation means the x value is negative. This rule doesnt apply to the k value within the equation, if the k value is a positive that means the y value stays a positive and vice versa.
Finding the Axis of Symmetry is even easier then finding the vertex of the equation. The AOS is the x-coordinate in the vertex. This is because the axis of symmetry is a vertical line that divides the parabola into two congruent halves. The axis of symmetry always passes through the vertex of the parabola. The x-coordinate of the vertex is the equation of the axis of symmetry of the parabola
Optimal Value
The optimal value which is the y-coordinate, is equal to the k value within the equation
Here's a video that helps explain this topic even more
Consider This...
The vertex of a parabola is at (-4,8). One of the x-intercepts is at (2,0). What is the equation of the parabola?
First let's determine what information is given to us.
-
we have been given our h value and our k value
-
we have been given an x-intercept
Secondly, let's substitute the information provided into the equation
y=a(x-h)2+k
So lets first put the h and the k value
y=a(x+4)2+8
Now we can place in our x-intercept
y=a(2+4)2+8
You can see that we are only missing our a value, which we will find using algebra
0=a(36)+8
-8= a36
-8/36= a36/36
-1/9=a
Therefore the equation for this parabola is
y= -1/9(2+4)2+8
Designed By Priyanka Madhok
bottom of page